Origin of Arabic Numerals - Was It Really for Counting Angles?
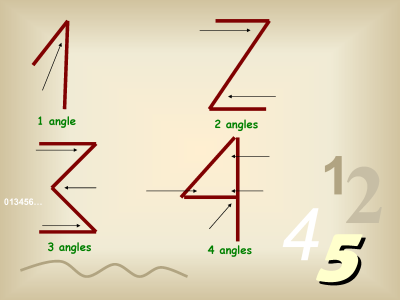
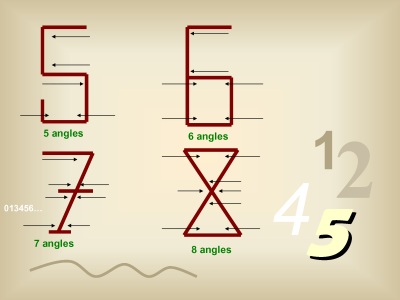
I received an e-mail forward the other day, which contained a PowerPoint presentation giving the supposed origin of Arabic numerals. It claimed that when each number is written with only straight lines, the number of angles created is the same as the quantity being represented. The text accompanying the presentation made the additional claim that these numerals have remained unchanged for thousands of years.
That explanation is completely false. I won't go into detail on the origins of the numerals in this entry since there are already sources that cover this. There are several Wikipedia articles that overlap on this subject. The first one below is probably best for the history of the symbols. The second one has some good general information. The third one has a good picture of the first known use of Arabic numerals in Europe.
Hindu-Arabic Numeral System
Arabic Numerals
History of the Hindu-Arabic Numeral System
The unique feature of our numbering system, having each position represent a power of 10 (as opposed to a system like Roman numerals), developed some time between the first and sixth centuries. Most of the symbols in that early system came from Brahmi numerals (which themselves came from earlier sources), but a few seem to have come from other sources, such as Buddhist inscriptions. The symbol for zero is an exception, having been invented around the same time as the decimal numbering system. There's some question to how those Brahmi symbols were developed and what they originally represented, but it certainly wasn't for counting angles. One, two, and three are pretty easy, since, like Roman Numerals, they were simply one, two, or three lines (even in Arabic numerals, one, two, and three all seem to have been originally related to simple counting - follow those links). The other symbols may have come from their alphabet.
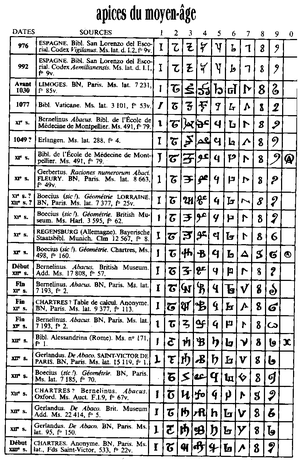
At any rate, the symbols have evolved quite a bit over the centuries, going down different paths in the different regions where they've been used. I've borrowed one of the images from Wikipedia and posted it below, a table compiled in 1757 showing various usages of numerals in European history (go to Wikipedia for a higher resolution image). Not only would we have a hard time reading the numbers from other regions of the world today, we'd have a hard time reading some of the earliest European uses.
Here's the full e-mail that I received, with the PowerPoint converted into a series of images. Scroll down for a bit more commentary following this.
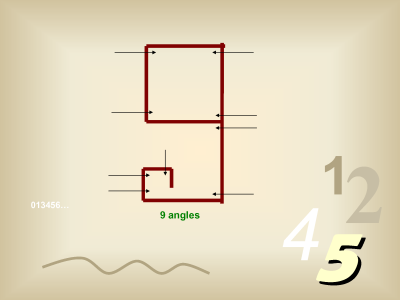
How numerals 0 - 9 got their shape - InterestingDo you know why numbers look like they do? Someone, at some point in time, had to create their shapes and meaning.
Watch this short presentation and then you will know how our Arabic numbers were originally created a very long time ago and what logic the people that created them used to determine their shapes. It is really very simple and quite creative? You have to admire the intelligence of a person that created something so simple and perfect that it has lasted for thousands and thousands of years and will probably never change?
When the presentation gets to the number "seven" you will notice that the 7 has a line through the middle of it. That was the way the Arabic 7 was originally written, and in Europe and certain other areas they still write the 7 that way. Also, in the military, they commonly write it that way. The nine has a kind of curly tail on it that has been reduced, for the most part nowadays, to a simple curve, but the logic involved still applies.
I've already given sources showing that this explanation is false, as are the claims in the accompanying text, but let's have a bit of fun looking at the numbers.
First, look at the 4. That is how 4 is typed, but most people I know don't write it by hand in that way. Most write it as:
On the 5, notice the little additional line on the lower left to make the count come out to 5.
Who writes their 7s that way? I know many people put the line through it, but who puts the serifs on the bottom?
The 9 takes the cake, though. It really takes some stretching to imagine that the 'primitive' form of 9 would look like that.
If there's one thing that all our letters and numbers have in common, it's that they're relatively simply - just a few strokes to create each one. That's the way you'd want it for an efficient handwriting system. It's really tough to imagine that 9 ever having been commonly used.
I suppose that one reason this e-mail continues to make the rounds is summed up in the second sentence of the first paragraph in that e-mail, "Someone, at some point in time, had to create their shapes and meaning." Many people like to think that something as important as our numerals had to be deliberately invented, that it couldn't have come about by a haphazard process. But, that's the way so many things have been developed, especially in language.
The actual history of our numerals really is pretty interesting. It's a shame for the people who miss out on that by getting the simple folk etymology in this e-mail.
Comments
Though your article is compelling, your support comes from Wikipedia: an altogether unreliable open-source encyclopedia, frequently accosted by the ignorance of the masses. While I, too, have received a similar email, let's not go about disproving the theory with a source that has the same crediblilty as Dr. Seuss's Medical Journal.
Posted by: Kenneth | November 16, 2009 11:07 AM
My previous post came across as coarse. Sorry about that. If you do find a reputable source of information, be sure to let us know! I've since accessed a couple of encyclopedias and other, more exhaustive tomes of useless information, but have since discovered that guesswork and conjecture are the driving forces behind many of these theories.
Posted by: Kenneth | November 16, 2009 02:50 PM
Wikipedia is open to be edited by anybody, which certainly raises suspicions about its quality. However, in practice, it ends up being fairly reliable, probably due to the fact that it has a core group of dedicated editors who police the work of less informed contributors. There was a study conducted by Nature a few years ago comparing Wikipedia to Encyclopædia Britannica. While Wikipedia was a little less accurate, it wasn't even by an order of magnitude. You have to have a subscription to Nature to read the original article, but here's a summary of it from cnet news.
In my experience, I've found Wikipedia to be pretty reliable, especially on non-controversial or apolitical topics. Plus, Wikipedia's gotten pretty good about referencing and citations. You can always scroll to the bottom of an article and go to the sources yourself, if so inclined. If you're planning on doing in depth analysis of a topic, Wikipedia can be a good starting point for this reason.
As for another common complaint about Wikipedia, the problem of referencing it as a source when it's constantly changing, you can reference static versions of pages. For example, here are static links to each version of the article, Hindu-Arabic numeral system, since I first posted this blog entry. With a little digging, you can find explanations for each revision.
13 Nov
10 Nov
3 Nov
3 Nov
30 Oct
28 Oct
28 Oct
28 Oct
29 Sept
If your problem is with encyclopedias in general, then I don't have much advice. It's true that encyclopedias contain mistakes, but so does every source of information. It's up to every individual to evaluate information from any given source, and compare it to other sources. There's no simple way to get 100% accurate information. Actually, that's one of the reasons why I like Wikipedia. Conventional print encyclopedias have a hidden editorial process. Wikipedia puts it out there in the open, making it easier to evaluate information on the more controversial topics.
Besides, this is a blog entry, on a folk etymology that seemed especially silly. I didn't think world class research was necessary.
Posted by: Jeff | November 17, 2009 02:18 PM
Wikipedia -- what it is worth? I hear assaults on Wikipedia from a few sources scoffing at the way it was started, how it is maintained, etc. In truth, it is the very open nature and wide visibility of Wikipedia which makes it one of the most reliable sources of information on the planet! Becuase so many people including "experts" access its info or are asked to review and comment on it -- the info gets a very wide and thorough going over. "Controversial" sections are always marked as such to alert readers that differing points of view exist -- also any articles that seem to push a bias are flagged, and new editors or contributors have been assigned to many older entries whcih generated frequent comment. All in all I continue to use Wikipedia as a first source for overview and find it often quite thorough and better written than many other sources.
Posted by: John Barker | January 9, 2010 10:25 AM
Putting Wikipedia's general accuracy aside, Wikipedia is sufficient for this specific task because it gives many alternate forms of the numbers today, and from history.
- Arguing that even if some of Wikipedia's number forms are incorrect, not all of them are. This alone refutes the slide show.
- Arguing that even if all of Wikipedia's forms are incorrect,
- They will be corrected at some time by somebody. (How about you?)
- They can be validated by other sources. (Did you find one inaccuracy in the numbers case?)
- The burden of proof is small. Jeff, with or without Wikipedia, doesn't have to assert the real truth of today's number forms (nor did he.) He merely pointed out that the slide show was false.
- Wikipedia was not Jeff's sole argument. Remove Wikipedia, and his argument for a hoax is still persuasive.
Overall, my feeling is Kenneth hijacked the numbers conversation with a Wikipedia soapbox. Did he refute that the slide show is a hoax? No. Did he even bring one error to light in the cited Wikipedia pages? No.Posted by: Aegean BM | February 25, 2010 02:55 PM
I just wanted to say thanks for taking the time to show us that this was false. I would hate for my children to go around thinking that was the way numbers used to be written. Yes, I quit believing at 9 because I thought that was a stretch myself but my children might not have thought so. I think its good that this is out there for my children to find when they receive emails that are false. Thanks to whomever it is who did take to time to search..no matter what way you researched!!
Posted by: interestedinnumbers | February 25, 2010 05:48 PM
So your blog came up with I did a litte google search about that power point that someone had forwarded to me. It just didn't seem right, and didn't sit right with me, so I thought I would try to see if anyone else had thought so too. I see you got this a while back, yet here I am to comment now. I liked your point about the scripted way of writing 7's. When I saw that it made me wonder why the 1 didn't have serifs at the bottom as they claimed the seven did.
Posted by: Jen | June 24, 2010 01:06 AM
Thanks for the research Jeff. I love forwarding mails but sometimes a mail just doesn't sit right! I googled "how numerals got their shape" and the first hit was this blog... will not be forwarding the mail
Posted by: Henri | July 6, 2010 06:45 AM
Kenneth got owned.
Posted by: Brandon | July 20, 2010 08:23 PM
Though I cannot confirm the angle theory, it has always been strange to me that nearly all information must be verified from a euro-centric view. Historically, however, much of the early knowledge that Europeans had came from Africa, Asia, and what we now call the Middle East. With that in mind, the angle story is believable though unconfirmable.
Posted by: Franklin | July 23, 2010 10:58 AM
Franklin,
I'm not sure I follow your argument. I explained how the numerals did come from regions outside western Europe. The first link from Wikipedia explicitly states, "the widespread Western 'Arabic numerals' used with the Latin, Cyrillic, and Greek alphabets in the table below labelled 'European', descended from the 'West Arabic numerals' which were developed in al-Andalus and the Maghreb." I don't see how that's a Euro-centric explanation.
Besides, when you look at the Arabic-Indic numerals, I think it's pretty clear that the symbols for 1, 2, and 3 came from counting tic marks, and that the Western versions are simply rotated 90º, and losing the 'tail' from the 3.
It's not just that the angle method is unconfirmable, it's definitely unbelievable as well.
Posted by: Jeff | July 23, 2010 04:56 PM