Here is a proof of the Pythagorean Theorem. This is the well know formula:
a² + b² = c²
where a and b are two sides of a right triangle, and c is the hypotenuse.

Below is a figure showing the geometric proof of the theorem. Following the figure is an explanation of each step.

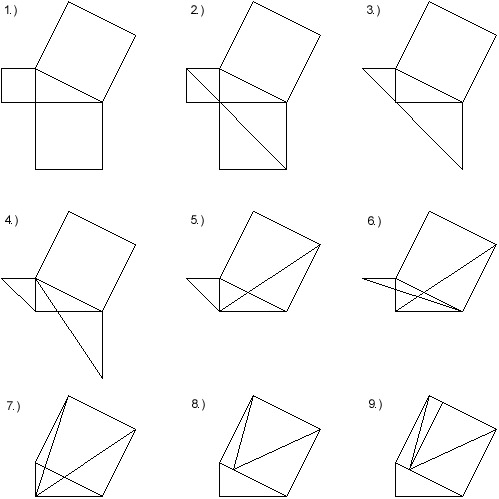
1.) Start by making squares on each side of a triangle, with the length of the side of a square being the length of a side of the triangle. The areas of the three squares, then, are a², b², and c².

2.) Divide the two squares not on the hypotenuse into triangles.

3.) Ignore two of the newly created triangles for right now. Just remember that their area is equal to the area of the triangles that will be used.

4.) Slide the vertex of the one triangle parallel to its base, so that the triangle shares a side with the square on the hypotenuse. Since the vertex was moved parallel to the base, the area has not been changed.

5.) The triangle can now be rotated 90º to be as shown. The sides are equal in length to the sides they share with the triangle and square.

6.) Slide the vertex of the small triangle in the same manner as was done in step 4 for the larger triangle.

7.) Rotate this triangle 90º.

8.) Slide the vertices of the two triangles parallel to the sides of the square, until the vertices lie on the hypotenuse of the original triangle. Once again, since the vertices are being moved parallel to the bases of the triangles, the area is not changed.

9.) Remember those two triangles that we temporarily removed in step 3. Well, now we can put them back in. We know that the manipulations we performed on the the two triangles that we used didn't change their area, so we can put in their mirror images to make up for the triangles that were removed. So, the two smaller triangles in step 9 still have the same area as the the two smaller triangles in step 2. The same is true for the larger two triangles. And we can see that the area of those 4 triangles is the same as the square of the hypotenuse. In other words,
a² + b² = c²